Почему резина лопается при резком растяжении? Математическая модель объяснила эффект острых трещин
Вы когда-нибудь быстро растягивали резиновый жгут или отрывали кусок гелевого пластыря? Сначала материал поддается, тянется, но в какой-то момент происходит резкий, почти мгновенный разрыв. Физики долго не понимали, почему этот процесс происходит именно так. Эксперименты показывали, что перед тем, как трещина начинает быстро двигаться, ее кончик становится очень острым.
Стандартные теории механики этого не предсказывали. Они говорили, что трещина должна иметь гладкую параболическую форму, а не острый конец. Было понятно, что для мягких материалов, таких как резина и гели, нужны другие расчеты.

Новое исследование ученых из Японии дает на этот вопрос математический ответ. Они вывели формулу, которая описывает форму движущейся трещины. Эта формула объясняет, почему скорость делает линию разлома острой.
Почему парабола не подходит?
Классическая теория разрушения отлично работает для твердых материалов, например, стекла или металла. По этой модели, кончик любой трещины должен быть похож на параболу. На этом принципе основано множество инженерных расчетов.
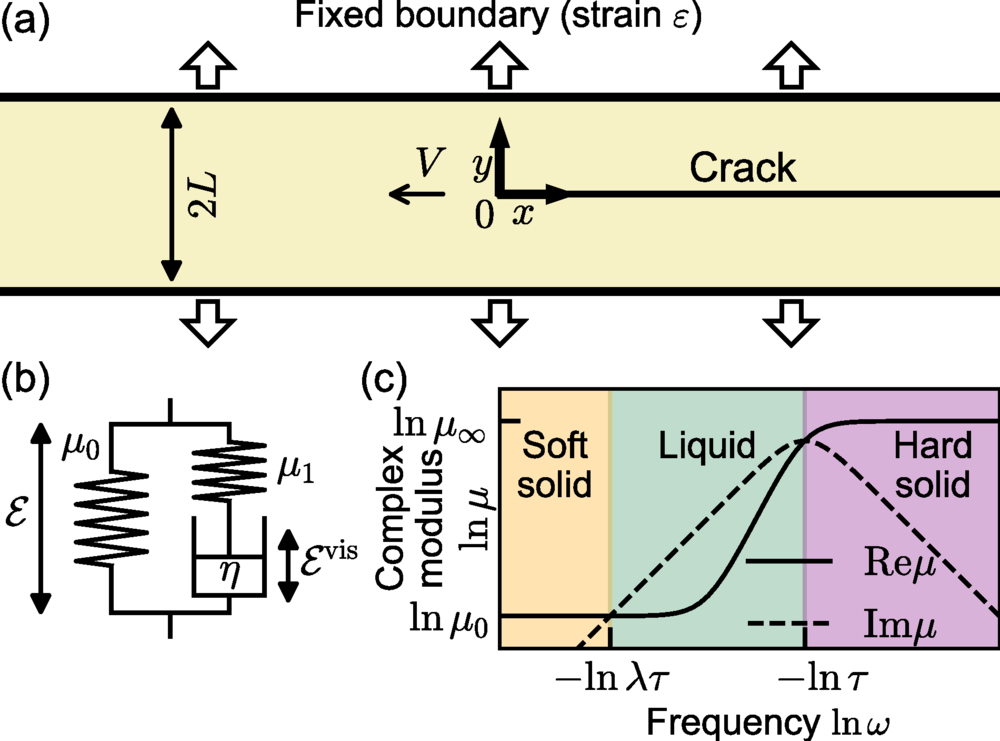
Но резина — другой материал. У нее есть свойство вязкоупругости. Это означает, что материал ведет себя и как упругое тело (возвращается к своей форме), и как вязкая жидкость (сопротивляется быстрому движению). Реакция такого материала зависит от скорости, с которой к нему применяют силу.
Именно из-за этого свойства старая теория не работала в случае с резиной. Наблюдения показывали обратное: чем быстрее идет трещина, тем острее ее кончик. Требовалась новая теория, которая бы учитывала время.
Гипотеза о «трубе»: верная, но без доказательств
Такую идею предложил в 1990-х годах ученый Пьер-Жиль де Женн. Он предположил, что профиль трещины в вязкоупругом материале должен быть похож на раструб трубы.
Его гипотеза состояла в том, что у разлома есть три отдельные зоны, и каждая описывается своей степенной функцией:
- Далеко от кончика: материал ведет себя как мягкое твердое тело. Профиль трещины здесь параболический (показатель степени 1/2).
- Ближе к кончику: здесь проявляются свойства жидкости. Профиль становится очень острым (показатель степени 3/2).
- У самого кончика: на микроуровне материал снова твердый, но уже более жесткий. Профиль опять параболический (показатель 1/2).
Эта идея хорошо описывала общую картину, но у нее был недостаток. Де Женн пришел к этим выводам на основе общих рассуждений об энергии. У него не было строгого вывода этой формы из уравнений механики. Его модель оставалась концепцией без математического фундамента.
От гипотезы к формуле: что показало новое исследование?
Этот пробел заполнила работа японских ученых. Они уже ушли от общих принципов, и провели вычисления. На основе известной модели вязкоупругости они получили точное математическое выражение, которое описывает форму трещины при ее движении с постоянной скоростью.
Их формула полностью воспроизвела модель де Женна. Она показала те же три зоны с теми же степенными показателями: 1/2, 3/2 и снова 1/2. Теперь гипотеза, которой было почти тридцать лет, получила математическое подтверждение.
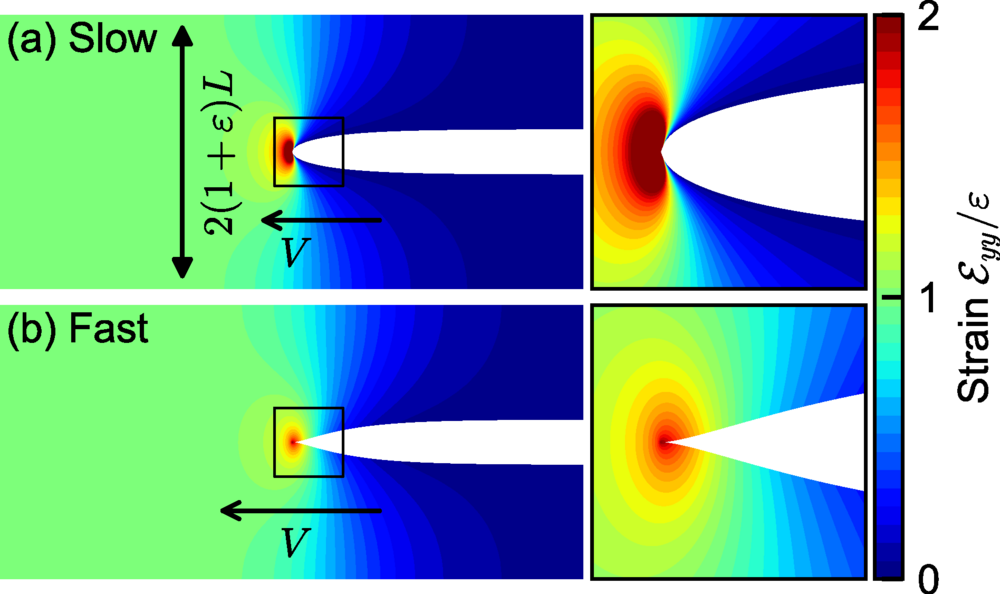
Но ученые получили и новые сведения. Их формула показала старую теорию ее в динамике, продемонстрировав, как профиль трещины зависит от скорости ее движения.
Когда скорость трещины увеличивается, средняя, «острая» зона с показателем 3/2, становится больше. Если трещина движется медленно, ее форма близка к параболе. Если трещина движется быстро, в ее форме преобладает острый конец.
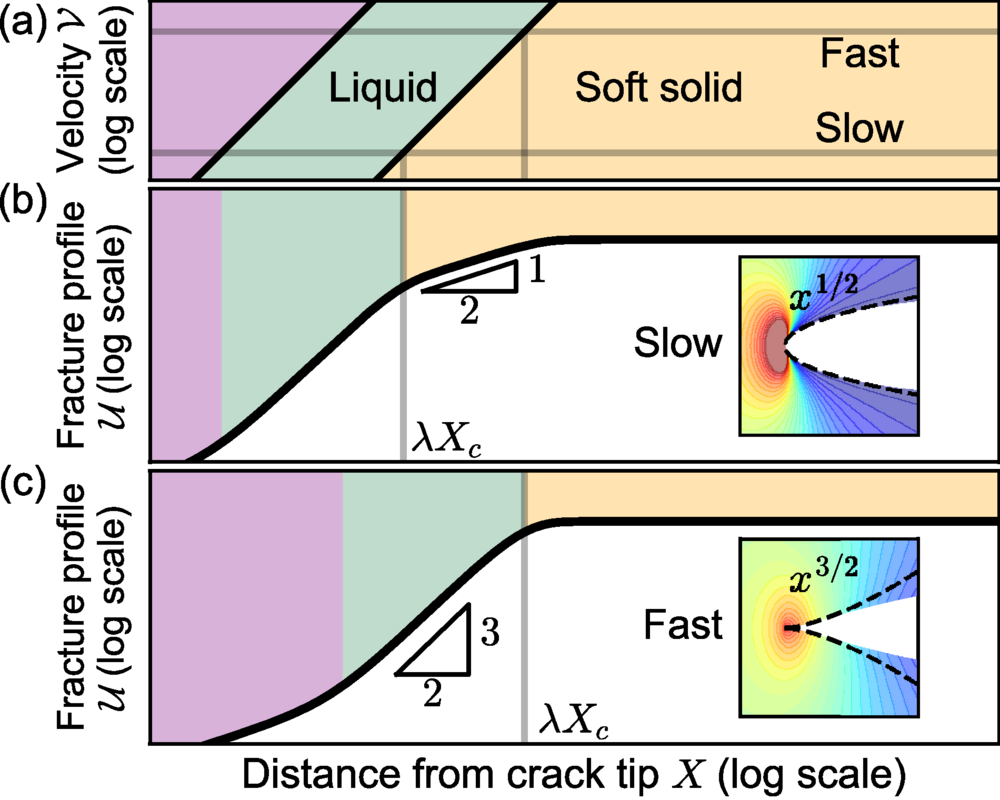
Это и есть прямая связь между скоростью и резкостью. Быстрое разрушение начинается, когда острая зона разлома вырастает настолько, что материал больше не может рассеивать энергию.
Какое у этого практическое значение?
Это дает инженерам полезный инструмент, ведь знание того, как скорость влияет на форму разлома, помогает создавать более прочные полимеры.
Если известно, что заострение трещины — это следствие вязкоупругих свойств, можно создавать материалы, которые будут этому сопротивляться.













