Квантовый компьютер наконец-то заработает надежно? Впервые продемонстрирована успешная коррекция ошибок для кудитов

18 май 2025, 21:14

Квантовые компьютеры — это почти магия, не так ли? Машины, обещающие революцию в медицине, материаловедении, криптографии, да где угодно! Но, как и у всякого уважающего себя волшебника, у них есть своя ахиллесова пята. В данном случае — это хрупкость квантовой информации. Любой «чих» извне, любой шум, и вот уже драгоценные квантовые биты, или кубиты, теряют свои волшебные свойства. И тут на сцену выходит квантовая коррекция ошибок (ККО) — без нее все эти квантовые чудеса рискуют остаться красивой теорией. Недавно исследователи из Йельского университета сделали нечто, что может серьезно продвинуть нас на пути к надежным квантовым вычислениям. Их работа, опубликованная в престижном журнале Nature, впервые демонстрирует успешную коррекцию ошибок для более сложных «родственников» кубитов — кудитов. Звучит интригующе? Давайте разбираться.

Больше — значит лучше? Знакомьтесь, кудиты!

Чтобы понять всю соль открытия, нужно сделать небольшой экскурс в квантовые «джунгли». Большинство из нас слышало о кубитах. Это как обычные биты в вашем компьютере (0 или 1), но с квантовым «бонусом»: они могут быть и 0, и 1 одновременно, благодаря явлению суперпозиции. Это дает им невероятную вычислительную мощь. Пространство всех возможных состояний кубита называется гильбертовым пространством. И вот тут-то и начинается самое интересное: чем оно больше, тем шире размах для квантовых «фокусов», включая ту самую коррекцию ошибок.

Иллюстрация
Автор: ИИ Copilot Designer//DALL·E 3 Источник: www.bing.com

А что если пойти дальше? Что если наша квантовая единица будет иметь не два, а три, четыре или даже больше состояний? Вот тут-то и появляются кудиты (от «quantum digit»). Кутрит, например, может находиться в трех состояниях, кукварт — в четырех. Представьте, какой простор для маневра! Большее гильбертово пространство на одну частицу означает потенциально более эффективное кодирование информации и, как следствие, более компактные и, возможно, более мощные квантовые процессоры. Ученые уже давно присматриваются к кудитам, пытаясь «строить» их на фотонах, ультрахолодных атомах и сверхпроводящих схемах. Ведь такие системы сулят упрощение создания квантовых вентилей, запуска алгоритмов и даже моделирования очень уж мудреных квантовых систем.

а, Схема экспериментальной установки. b, Геометрическая структура операторов смещения, определяющих одномодовый квадратный GKP-код. c, Схема для одного раунда стабилизации GKP-кудита с конечной энергией, обобщающая протокол SBS¹³. Большой ECD-вентиль⁴⁸ с амплитудой ℓd,Δ = √πd cosh(Δ²) приблизительно равен длине стабилизатора. Малые ECD-вентили с амплитудой εd/2 = √πd sinh(Δ²)/2 учитывают размер огибающей Δ. В конце раунда SBS j, фаза резонатора обновляется как ϕj (см. Методы, здесь и далее ссылки обращаются к оригинальному исследованию). d, Измеренная действительная часть характеристической функции максимально смешанного GKP-кудит состояния для d = от 1 до 4 при Δ = 0,3, приготовленного путем выполнения 300 раундов SBS, начиная с резонатора в его вакуумном состоянии |0⟩.
Автор: Brock, B.L., Singh, S., Eickbusch, A. et al. Источник: www.nature.com

Зачем вообще нужна эта коррекция ошибок?

Представьте, что вы пытаетесь донести очень важное и тихое сообщение через шумную площадь. Без специальных методов (крикнуть погромче, использовать жесты, повторить несколько раз) ваше сообщение, скорее всего, исказится или вовсе потеряется. Квантовая информация еще более капризна. Любое взаимодействие с окружающей средой, будь то случайное электромагнитное поле или даже просто тепловое излучение, может «спугнуть» хрупкие квантовые состояния. Это называется декогеренцией.

Именно поэтому квантовая коррекция ошибок — это не просто «фишка», а жизненная необходимость. Она работает по принципу, немного похожему на то, как мы исправляем ошибки в классических данных: избыточность. Информация кодируется не в одном кубите/кудите, а в нескольких, и специальные алгоритмы отслеживают и исправляют возникающие «опечатки». Однако до сих пор львиная доля экспериментальных работ в этой области была сосредоточена на старых добрых кубитах. Кудиты как-то оставались на вторых ролях, ожидая своего звездного часа.

a, Приготовление собственных состояний Паули кутрита |P₀⟩₃ с Δ = 0.32. b, Схема для измерения кутрита в базисе оператора Паули P₃ с использованием вспомогательного кубита (анциллы), где θ₀ = 2 arctan(1/√2). Первое измерение различает состояние |P₀⟩₃ и подпространство {|P₁⟩₃, |P₂⟩₃}, тогда как второе различает |P₁⟩₃ и {|P₀⟩₃, |P₂⟩₃}. Сферы Блоха изображают траектории, проходимые анциллой, когда кутрит находится в каждом собственном состоянии Паули. c, Обратное воздействие (бэканализ) измерения Паули кутрита в базисе Z₃, примененное к максимально смешанному состоянию кутрита. d, Распад собственных состояний Паули кутрита |P₀⟩₃ в рамках оптимизированного протокола QEC. Пунктирные черные линии указывают вероятность 1/3. Сплошные серые линии представляют собой экспоненциальные аппроксимации. Слева направо мы получили γ⁻¹X₀ = 1,153 +- 13 µs, γ⁻¹Z₀ = 1,120 +- 15 µs, γ⁻¹XZ₀ = 743 +- 10 µs и γ⁻¹X²Z₀ = 727 +- 11 µs.
Автор: Brock, B.L., Singh, S., Eickbusch, A. et al. Источник: www.nature.com

Йельский прорыв: когда теория становится практикой

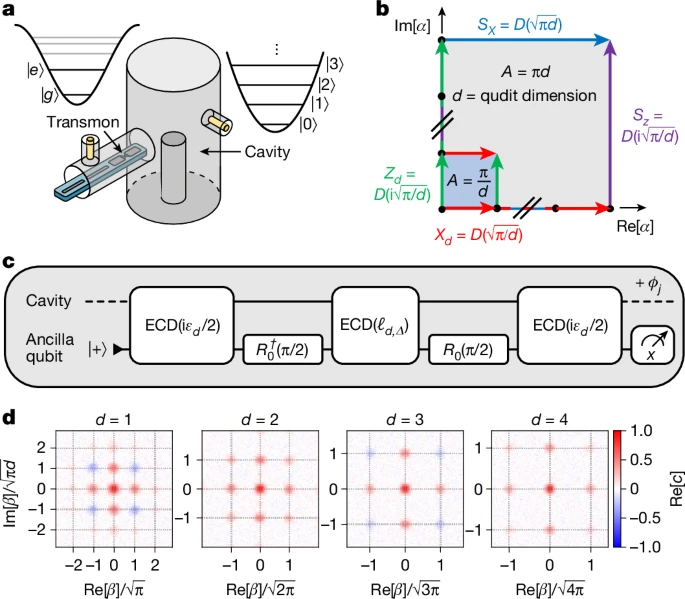
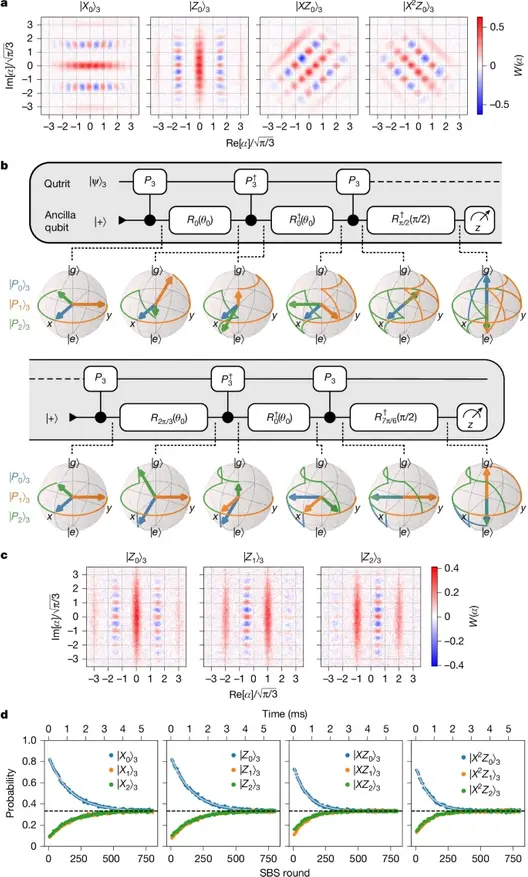
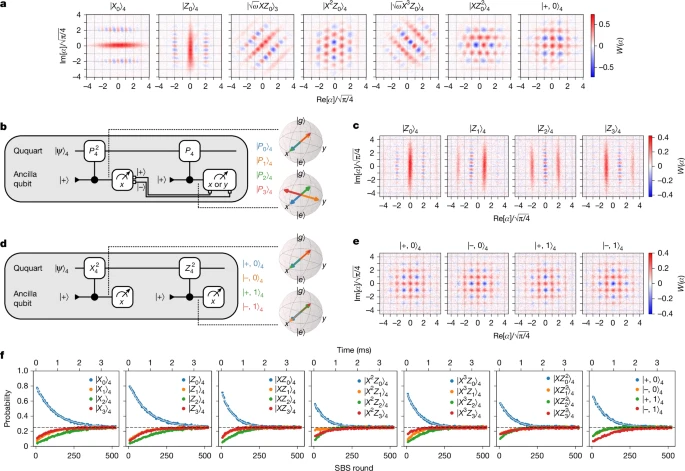
И вот тут-то на сцену выходят исследователи из Йеля. Они не просто теоретизировали, а взяли и впервые экспериментально показали, что ККО работает и для кудитов — конкретно, для кутрита и кукварта. Как им это удалось? Они использовали так называемый бозонный код Готтесмана-Китаева-Прескилла (сокращенно ГКП). Это довольно хитрая схема, позволяющая кодировать квантовую информацию в состояниях гармонического осциллятора (например, электромагнитного поля в резонаторе).

Но просто взять код — полдела. Нужно было научить систему эффективно исправлять ошибки. И тут на помощь пришло машинное обучение, а точнее — обучение с подкреплением. Представьте себе умного ученика, который методом проб и ошибок находит лучший способ выполнить задачу. Примерно так же алгоритм «натаскивал» систему на оптимальную коррекцию ошибок и управление квантовыми вентилями.

Что особенно важно, эксперимент не просто сработал, а преодолел так называемую «точку безубыточности» для коррекции ошибок. Проще говоря, система начала исправлять больше ошибок, чем вносила сама в процессе работы. Это огромный шаг, демонстрирующий практичность и аппаратную эффективность подхода, который становится возможным благодаря «богатству» гильбертова пространства кудитов.

a, Приготовление собственных состояний Паули кукварта |P₀⟩₄ и состояния четности |+, 0⟩₄ с Δ = 0.32. b, Схема для измерения кукварта в базисе оператора Паули P₄ с использованием вспомогательного кубита (анциллы). Первое измерение различает четные и нечетные состояния |Peven/odd⟩₄, а второе измерение различает два оставшихся состояния. Сферы Блоха изображают траектории, проходимые анциллой, когда кукварт находится в каждом собственном состоянии Паули. c, Обратное воздействие (бэканализ) измерения Паули GKP-кукварта в базисе Z₄, примененное к максимально смешанному состоянию кукварта. d, Схема для измерения кукварта в базисе четности {|+-, m⟩₄: m = 0, 1}, где X²₄|+-, m⟩₄ = +-|+-, m⟩₄ и Z²₄|+-, m⟩₄ = (−1)m|+-, m⟩₄. Первое измерение определяет собственное значение X²₄, а второе определяет собственное значение Z²₄. e, Обратное воздействие (бэканализ) измерения четности GKP-кукварта, примененное к максимально смешанному состоянию кукварта. f, Распад собственных состояний Паули кукварта |P₀⟩₄ и состояния четности |+, 0⟩₄ в рамках оптимизированного протокола QEC. Пунктирные черные линии указывают вероятность 1/4. Сплошные серые линии представляют собой экспоненциальные аппроксимации. Слева направо мы получили γ⁻¹X₀ = 840 +- 8 µs, γ⁻¹Z₀ = 836 +- 9 µs, γ⁻¹XZ₀ = 519 +- 6 µs, γ⁻¹X²Z₀ = 507 +- 9 µs, γ⁻¹X³Z₀ = 571 +- 7 µs, γ⁻¹XZ²₀ = 562 +- 9 µs и γ⁻¹+, 0 = 607 +- 8 µs.
Автор: Brock, B.L., Singh, S., Eickbusch, A. et al. Источник: www.nature.com

Есть нюанс, но он того стоит?

Конечно, не все так безоблачно. Ученые честно признают: использование ГКП-кода для кудитов приводит к несколько большим потерям фотонов и более быстрой дефазировке (потере когерентности фаз). Это, в свою очередь, может немного сократить «срок годности» закодированной квантовой информации. Но, как говорится, есть и хорошая новость! Взамен этой небольшой «жертвы» мы получаем доступ к большему количеству логических квантовых состояний в одной-единственной физической системе. А это, знаете ли, дорогого стоит в мире, где каждый дополнительный надежный кубит (или кудит) — на вес золота.

Что дальше? А дальше — больше!

Так что же все это значит для нас, простых смертных, ждущих квантовой революции? Результаты йельских исследователей — это еще один важный кирпичик в фундамент надежных и масштабируемых квантовых компьютеров. Это не значит, что завтра у каждого дома появится квантовый компьютер, способный взломать все пароли мира или синтезировать лекарство от всех болезней. Но это демонстрация того, что мы движемся в правильном направлении.

Открытия такого рода подстегивают дальнейшие исследования. Возможно, именно кудиты с их расширенными возможностями станут ключом к созданию по-настоящему мощных квантовых машин. А это, в свою очередь, может привести к прорывам в самых разных областях: от разработки новых материалов и лекарств до создания сверхзащищенных систем связи и решения сложнейших вычислительных задач, которые сегодня нам даже не снятся.

Честно говоря, путь к полномасштабному квантовому компьютеру еще долог и тернист. Но каждая такая успешно решенная задача, как демонстрация коррекции ошибок для кудитов, приближает нас к цели. И это, безусловно, вселяет оптимизм. Похоже, кубитам скоро придется немного потесниться!

Опубликовано: Мировое обозрение Источник