Почему любое вращение можно отменить, если повторить его дважды: физики нашли способ управлять хаосом
Если запустить из катапульты камень сложной формы, он полетит по дуге, беспорядочно кувыркаясь и вращаясь в воздухе под действием начального импульса и сопротивления воздуха. Теперь задача: можно ли найти один-единственный регулятор — скажем, общий множитель, изменяющий интенсивность всех этих вращательных движений, — который заставит камень в конце пути приземлиться точно в той же ориентации, в которой он стартовал?
Интуиция подсказывает, что это практически невозможно. Слишком много переменных, и слишком хаотичное движение. Однако недавнее исследование физиков Жан-Пьера Экманна и Цви Тлусти говорит, что решение есть, но оно требует одного не очевидного условия: всю последовательность вращений нужно пройти не один, а два раза.

Это открытие напрямую касается управления квантовыми системами, спинами частиц и кубитами, где точный контроль ориентации является основой технологий будущего.
Что такое «прогулка» в пространстве вращений?
Сперва уточним понятия. Любое вращение в трехмерном пространстве определяется двумя параметрами: осью, вокруг которой происходит поворот, и углом этого поворота. Совокупность всех возможных вращений образует абстрактное математическое пространство.
Когда система (например, спин электрона в магнитном поле) претерпевает серию последовательных поворотов, она совершает своего рода «прогулку» или «траекторию» в этом пространстве. Начальная точка — это «отсутствие вращения», или, говоря математически, тождественное преобразование. Конечная цель — вернуться в эту же исходную точку.
Исследователи задались вопросом: можно ли взять любую, сколь угодно сложную «прогулку» и подобрать такой единый множитель λ (лямбда), который, будучи примененным ко всем углам поворота, вернет систему в ноль?
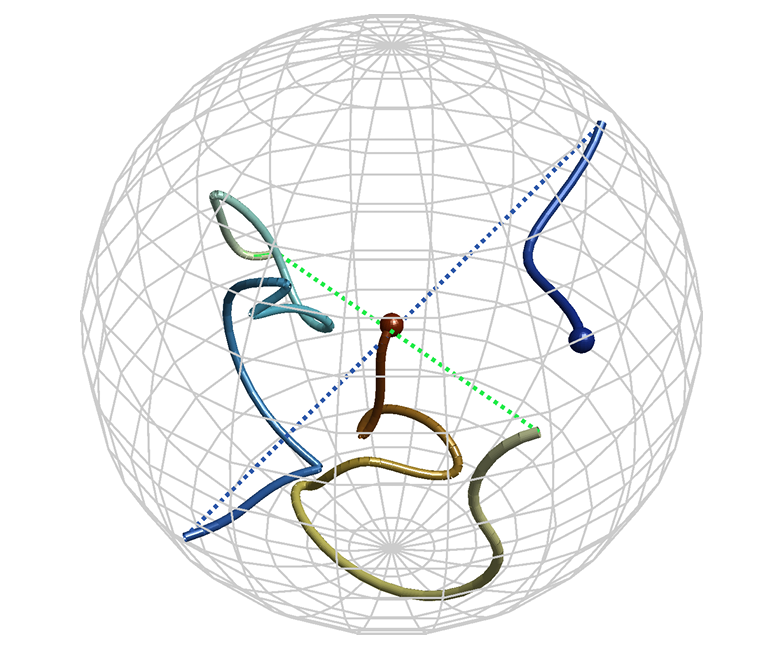
Почему один проход почти всегда обречен на провал?
Попытка сделать это за один проход сталкивается с фундаментальной проблемой вероятности. Ваша цель — попасть в крошечную, единственно верную точку. Шансы на успех, очевидно, стремятся к нулю.
Состояние «отсутствия вращения» — это одна-единственная точка в огромном пространстве всех возможных ориентаций. Статистический анализ, основанный на так называемой мере Хаара, показывает, что случайные вращения крайне неохотно группируются вокруг малых углов. Иными словами, вероятность того, что случайная последовательность поворотов сама по себе закончится в нулевой точке, практически равна нулю. Изменение одного-единственного параметра λ не меняет эту картину.
Магия удвоения: как 180 градусов все меняют
А теперь вводится ключевое изменение. Что, если мы потребуем, чтобы система вернулась в исходное состояние не после одного, а после двух одинаковых циклов вращения?
Математически это означает, что результат одного цикла должен быть таким, чтобы его повторение «обнуляло» само себя. Единственное нетривиальное вращение, обладающее таким свойством, — это поворот ровно на 180 градусов (или π радиан). Поверните объект на 180 градусов, а затем еще раз на 180 градусов вокруг той же оси — и он вернется в исходное положение.
И здесь все кардинально меняется. Наша цель — уже не одна-единственная точка «нулевого вращения», а любое вращение с углом в 180 градусов, независимо от оси. В пространстве вращений это не точка, а целая двумерная поверхность.
Попасть одним параметром λ в конкретную точку почти нереально. Но попасть на огромную поверхность — задача вполне выполнимая. Вероятность успеха резко возрастает. Авторы доказывают, что для практически любой исходной последовательности вращений всегда найдется такой множитель λ, который приведет итоговый поворот ровно к 180 градусам. А значит, второй такой же цикл вернет систему домой.
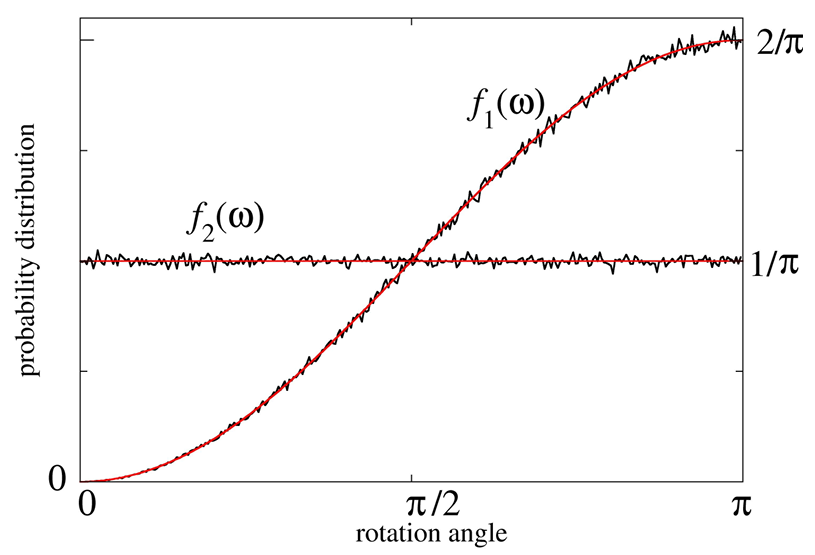
Как это доказывается?
За этим результатом стоит строгая математика. Исследователи использовали формулы Родригеса, которые описывают композицию вращений, и свели задачу к решению тригонометрического уравнения. Им нужно было доказать, что всегда можно найти такое λ, при котором итоговый косинус угла поворота станет равен нулю (что соответствует углу 180 градусов).
С помощью теоремы Минковского из области геометрии чисел они показали, что такое решение существует почти всегда. По сути, поиск нужного λ превращается в так называемую диофантову задачу — поиск целочисленных решений, которые удовлетворяют определенным условиям. И теорема гарантирует, что эти решения есть.
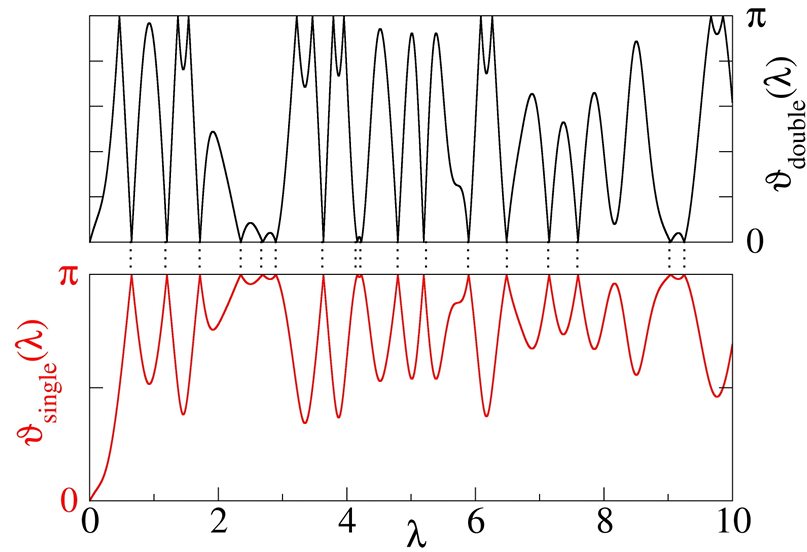
Работает ли это в других измерениях?
Этот ход — уникальное свойство нашего трехмерного мира. Авторы отмечают, что в пространствах с четырьмя и более измерениями он уже не работает.
Причина в усложнении самой природы вращения. В высших измерениях повороты происходят не вокруг одной оси, а одновременно в нескольких независимых плоскостях. Чтобы обнулить такой многокомпонентный поворот, нужно одновременно погасить несколько углов. Одного общего множителя λ для этого уже недостаточно. Потребовался бы отдельный регулятор для каждой плоскости вращения.
В итоге мы имеем дело с фундаментальным геометрическим свойством. Сложная, хаотичная последовательность вращений в 3D-пространстве содержит в себе скрытую возможность для обнуления. Нужно лишь правильно подобрать масштаб и дать ей пройти свой путь дважды. Это не интуитивно, но математически неизбежно. Это поможет найти новые подходы к точному управлению миром на квантовом уровне.