Откуда взялось число π и почему у него бесконечное количество знаков после запятой
Число π известно каждому школьнику, но его история и природа куда глубже простых формул из учебника или простого обозначения «3,14». Чтобы вас заинтриговать, добавлю, что после запятой у числа π буквально бесконечно знаков, которые никогда подряд не повторяются. А на сегодня известно 100 триллионов знаков после запятой. Но это, разумеется, далеко не все. Это число пронизывает геометрию, физику, астрономию и даже современные цифровые технологии. Чтобы понять, почему это так, нужно проследить путь числа π от древних цивилизаций до современных вычислений, и хотя бы поверхностно разобраться в его фундаментальных свойствах.

Что такое число π
Число π — это буквально отношение длины окружности к её диаметру. Его значение одинаково для любого круга, большого или маленького — неважно. Если разделить длину окружности на диаметр, всегда получится примерно 3,14159… Это неизменное отношение, и делает π фундаментальной математической константой.
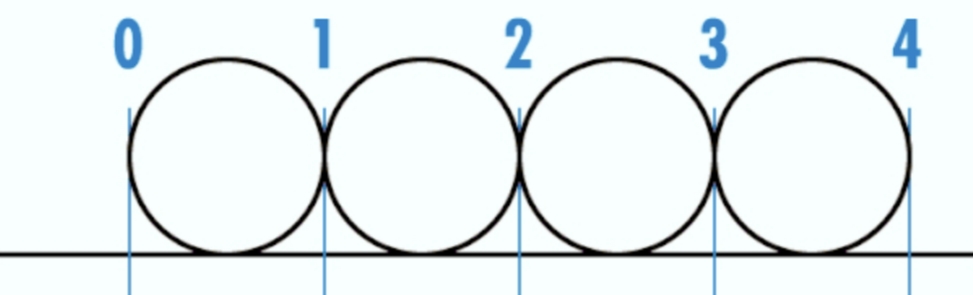
На уровне формул, π встречается в площади круга, объёме цилиндра, тригонометрии, гармонических процессах и множестве других областей. Оно отражает саму структуру пространства и форм, поэтому присутствует в свойствах волн, орбит планет и даже алгоритмах обработки сигналов. Но и это ещё не всё, константу π можно выразить как производную полупериода функции у = sin (x). Но в этой статье не об этом.
Почему у π бесконечное количество знаков после запятой
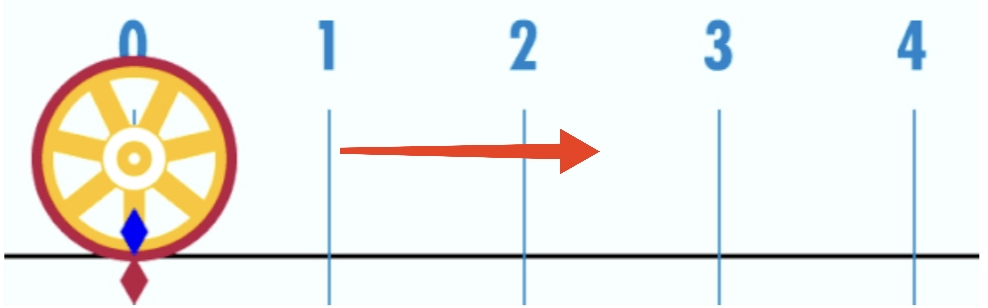
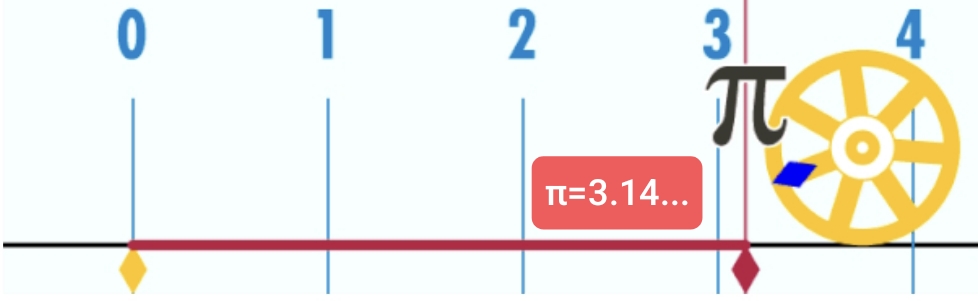
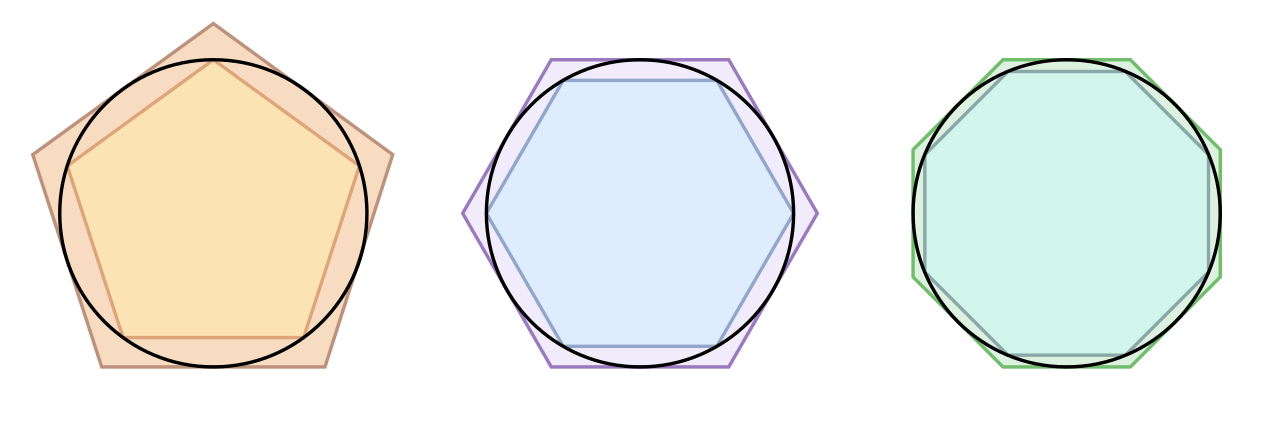
Десятичная запись числа π бесконечна и не периодична, потому что π называется иррациональным числом. Иррациональные числа невозможно выразить в виде простой дроби. В отличие от рациональных чисел, чьи дроби либо заканчиваются, либо переходят в повторяющийся цикл, иррациональные числа имеют бесконечную, не повторяющуюся последовательность цифр. Это далеко не все, но забегая вперёд, я постараюсь графически, с точки зрения геометрии, объяснить, почему число π имеет бесконечную запись. Для этого нужно, к примеру, бесконечно вписывать многоугольники в окружность, таким образом соотношение между длиной окружности и длиной вписанных многоугольников всегда будет меняться, но только после запятой. Таким образом, вписывая все новые и новые многоугольники, число π бесконечно изменяется после знака запятой.
Как и когда вычислили число π
Интересно, что настолько важная постоянная величина как π, насчитывает тысячи лет. Первые попытки вычислить отношение окружности к диаметру предпринимались ещё в Древнем Египте и Вавилоне. Египтяне использовали приближённое значение 3,16, а вавилоняне — 3,125. Более точные расчёты провёл Архимед в III веке до н. э. Он вписал и описал многоугольники вокруг окружности, и получил значение π между 3,1408 и 3,1429. Это тот метод, что изображён на фоне выше, в качестве графического объяснения. В Китае математик Лю Хуэй довёл точность до 3,14159, используя многоугольник с 3072 сторонами. Позднее индийские и арабские учёные продолжили работу, а в
Где применяется число π
Изначально кажется, что π исключительно геометрическое понятие, но его применение значительно шире. Именно поэтому изучению и расчетам числа π учёные уделяют так много времени. Оно используется в физике для описания волн, колебаний и электромагнитных процессов. В астрономии π встречается при расчётах орбит, расстояний и гравитационных взаимодействий. В инженерии оно необходимо для проектирования механизмов, вычисления объёмов резервуаров, оценки прочности конструкций и так далее. В цифровых технологиях π участвует в алгоритмах сжатия данных, компьютерной графике, моделировании и криптографии. Даже в статистике применяется π в нормальном распределении, лежащем в основе вероятностных моделей.

Заключение
Таким образом, число π — это больше, чем просто обычное неизменное соотношение. На базе этой константы построено много расчетов и технологий. Интересно то, что это число было рассчитано ещё в древнем мире, и на практике применялось ещё тысячи лет назад. На этом у меня всё, спасибо всем за внимание.
Источник: wikipedia
Источник: ru.freepik.com













