Можно ли найти конкретную каплю воды в стакане?
Почему капля воды, упавшая в стакан, исчезает навсегда: честный разбор
Вы капнули воду в стакан. И всё. Капля растворилась. Никакой магии — чистая физика. Но можно ли её вернуть? Теоретически — да. Практически — нет. И вот почему это не вопрос технологий, а фундаментальный закон природы.
Сначала цифры. Одна капля — это примерно 1020 молекул. В стакане — 1025. Разница в сто тысяч раз. Но дело не в количестве, а в тепловом движении. Молекулы воды носятся как бешеные. При комнатной температуре их скорость — сотни метров в секунду. Капля касается поверхности — и через секунду её молекулы уже размазаны по всему объёму.
Как это работает: от порядка к хаосу
Когда капля только падает, система упорядочена: молекулы капли собраны в одном месте, остальные — вокруг. Это состояние с низкой энтропией. Но тепловое движение моментально всё перемешивает. Диффузия идёт по градиенту концентрации — это второй закон термодинамики в действии.
Любая замкнутая система стремится к максимуму энтропии. Вернуть каплю — значит обратить этот процесс. А это равносильно нарушению стрелы времени.
Мой знакомый физик как-то сказал: «Если бы ты мог собрать молекулы обратно, ты бы смог и яичницу превратить обратно в яйцо». Смешно, но по сути верно.
Демон Максвелла: почему он не поможет
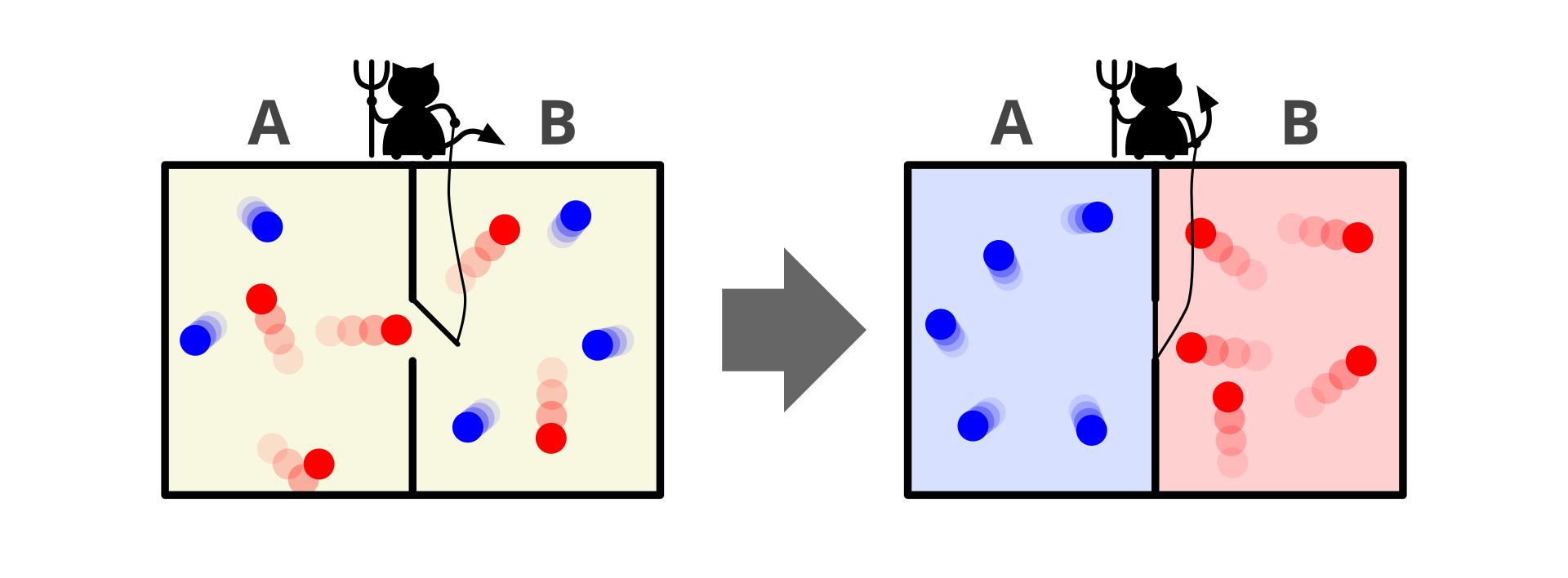
В XIX веке Джеймс Максвелл придумал мысленный эксперимент. Воображаемый демон сортирует быстрые и медленные молекулы, открывая перегородку. Теоретически это позволило бы уменьшить энтропию. Но на практике демон должен тратить энергию на измерение и сортировку — и это увеличивает общую энтропию системы.
Так что демон — лишь красивая иллюзия. Современные суперкомпьютеры могут моделировать поведение миллиардов частиц, но не триллионов. Даже если бы мы могли отследить каждую молекулу, квантовая неопределённость внесла бы ошибку.
| Параметр | Капля | Стакан |
|---|---|---|
| Число молекул | 1020 | 1025 |
| Время полного смешивания | ~0,1 с | ~10 с (без перемешивания) |
| Энтропия до | низкая | средняя |
| Энтропия после | максимум | максимум |
Личное наблюдение: что говорит природа
Недавно я заметил, как капля чернил растекается в чашке с водой. Сначала виден чёткий шлейф. Через минуту — равномерный синий цвет. И никакой «сборки» обратно. Флуктуации — случайные отклонения — возможны, но вероятность того, что все молекулы капли одновременно соберутся в одной точке, равна единице, делённой на число, большее, чем количество атомов во Вселенной.
Есть ещё один нюанс: броуновское движение. Частицы пыли в воде танцуют хаотично. Это наглядная демонстрация того, что молекулы никогда не остановятся. А значит, обратный процесс требует контроля над каждой частицей — а это практически невозможно.
Почему это важно: необратимость как фундамент
Второй закон термодинамики — не просто скучная формула. Это объяснение, почему мы стареем, почему чай остывает, почему всё вокруг стремится к равновесию. Попытка вернуть каплю воды — это попытка повернуть время вспять.
- Диффузия — необратима на макроуровне.
- Энтропия всегда растёт в замкнутой системе.
- Хаос — не баг, а фича природы.
Резюме от автора
Капля воды исчезла навсегда. Смиритесь. Это не вопрос технологий или суперкомпьютеров — это закон, на котором держится наш мир. Необратимость — не проклятие, а условие существования жизни. Если бы всё можно было «отмотать», не было бы ни времени, ни нас.
